Rompecabezas de la Torre de Hanói

El rompecabezas de la Torre de Hanói es un fascinante problema matemático y lógico que ha cautivado a personas de todas las edades durante generaciones. Su historia, soluciones y variaciones ofrecen una visión interesante tanto de la matemática como de la ingeniería de software.

Historia

El rompecabezas fue inventado por el matemático francés Édouard Lucas en 1883. Se cuenta una historia sobre un templo en la India en Kashi Vishwanath que contiene una gran sala con tres postes gastados por el tiempo, rodeada de 100 discos dorados. Los sacerdotes de Brahma, actuando bajo el mandato de una antigua profecía, han estado moviendo estos discos de acuerdo con las reglas inmutables de Brahma desde ese momento. Por lo tanto, el acertijo también se conoce como el rompecabezas de la Torre de Brahma. Según la leyenda, cuando se complete el último movimiento del rompecabezas, el mundo se terminará. No está claro si Lucas inventó esta leyenda o si se inspiró en ella.

Si la leyenda fuera cierta, y si los sacerdotes pudieran mover los discos a una velocidad de uno por segundo, utilizando el menor número de movimientos, completar la tarea les llevaría 2100 - 1 segundos, o aproximadamente 4.019 cuatrillones de años, que es aproximadamente 290.942 cuatrillones de veces la edad actual del Universo.

Existen muchas variaciones en esta leyenda. Por ejemplo, en algunos relatos el templo es un monasterio, y los sacerdotes son monjes. Se puede decir que el templo o monasterio se encuentra en diferentes partes del mundo, incluidos Hanói, Vietnam, y puede estar asociado con cualquier religión. En algunas versiones, se introducen otros elementos, como el hecho de que la torre fue creada en el comienzo del mundo, o que los sacerdotes o monjes solo pueden hacer un movimiento por día.

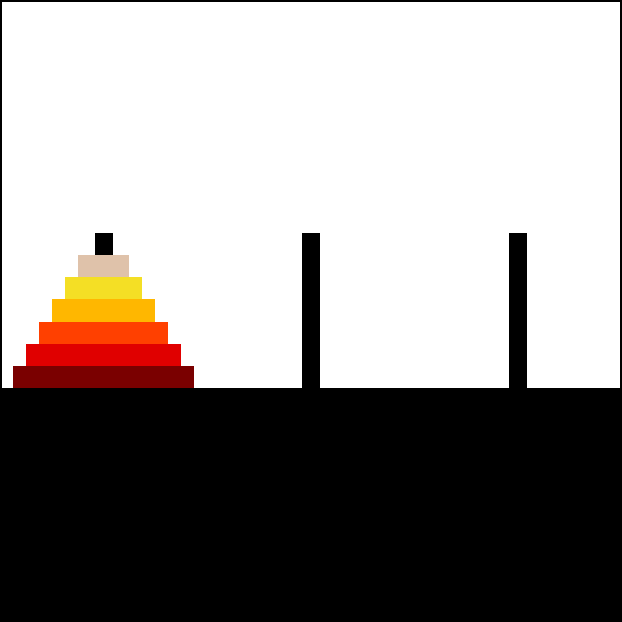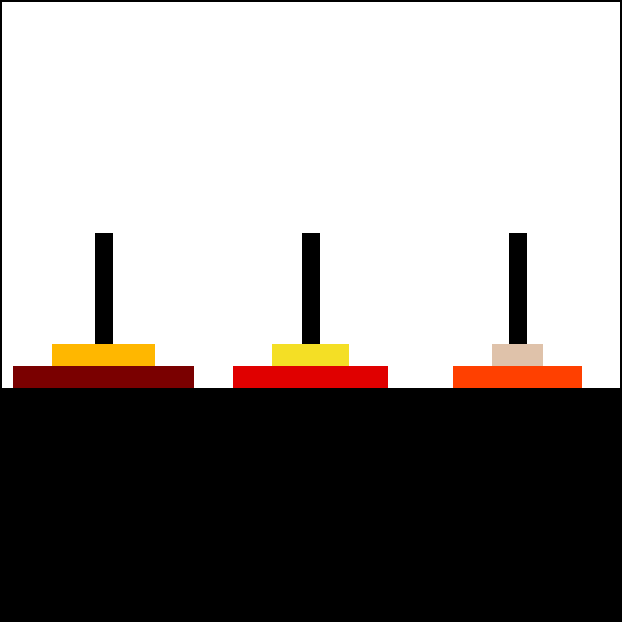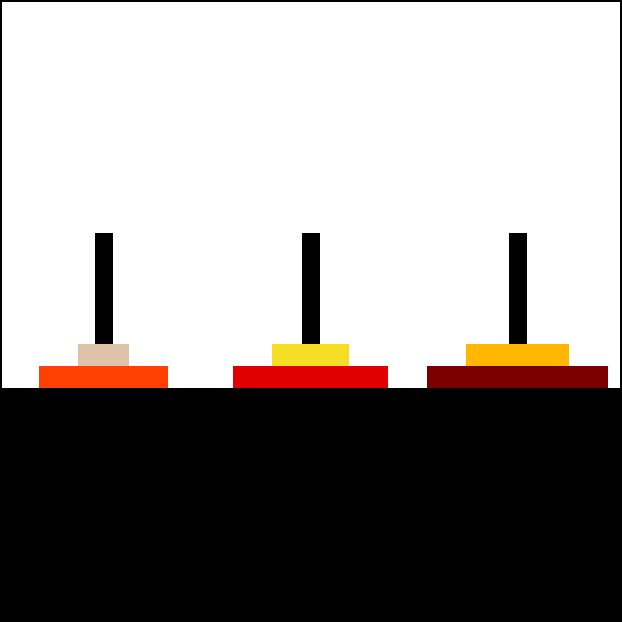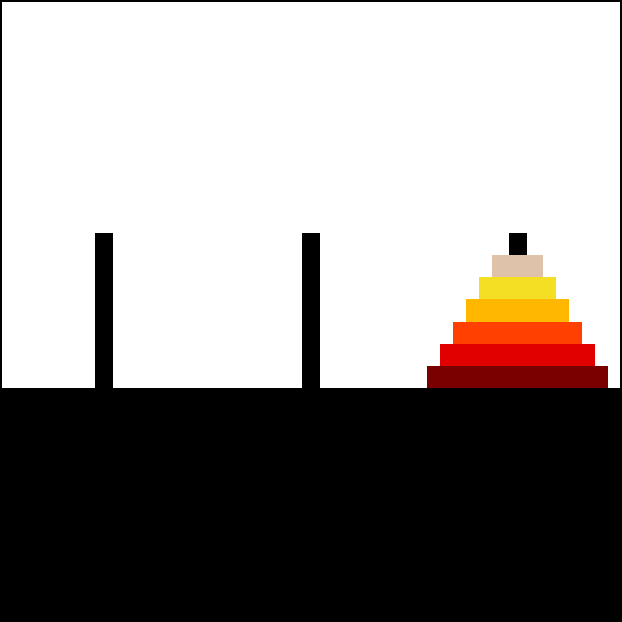
Resolución

La solución del problema de las Torres de Hanói es muy fácil de hallar, aunque el número de pasos para resolver el problema crece exponencialmente conforme aumenta el número de discos. Como ya se ha indicado, el número mínimo de movimientos necesarios para resolver un rompecabezas de la Torre de Hanói es 2n - 1, donde n es la cantidad de discos.

Una manera sencilla para saber si es posible terminar el "juego" es que si la cantidad de discos es impar, la pieza inicial irá al destino y si es par, irá al auxiliar.

Solución simple

Una forma de resolver el problema se fundamenta en el disco más pequeño, el de más arriba en la varilla de origen. En un juego con un número par de discos, el movimiento inicial de la varilla origen es hacia la varilla auxiliar. El disco n.o 2 se debe mover, por regla, a la varilla destino. Luego, el disco n.o 1 se mueve también a la varilla destino para que quede sobre el disco n.o 2. A continuación, se mueve el disco que sigue de la varilla origen, en este caso el disco n.o 3, y se coloca en la varilla auxiliar. Finalmente, el disco n.o 1 regresa de la varilla destino a la origen (sin pasar por la auxiliar), y así sucesivamente. Es decir, el truco está en el disco más pequeño.

Mediante recursividad

Este problema se suele plantear a menudo en programación, especialmente para explicar la recursividad. Si numeramos los discos desde 1 hasta n, si llamamos origen a la primera pila de discos, destino a la tercera y auxiliar a la intermedia, y si a la función la denomináramos hanoi, con origen, auxiliar y destino como parámetros, el algoritmo de la función sería el siguiente:

                    Algoritmo Torres de Hanói (Complejidad Θ(2𝑛−1))
                    Entrada: Tres pilas de números origen, auxiliar, destino, con la pila origen ordenada
                    Salida: La pila destino
                  
                    si origen == {1} entonces
                      mover el disco 1 de pila origen a la pila destino (insertarlo arriba de la pila destino)
                      terminar
                    si no
                      hanoi({1, …, 𝑛−1}, origen, destino, auxiliar) //mover todas las fichas menos la más grande (n) a la varilla auxiliar
                      mover disco n a destino //mover la ficha grande hasta la varilla final
                      hanoi(auxiliar, origen, destino) //mover todas las fichas restantes, 1...n–1, encima de la ficha grande (n)
                      terminar

El número de movimientos mínimo a realizar para resolver el problema de este modo es de 2n – 1, siendo n el número de discos.

Iterativa

Solución iterativa con 6 discos

Otra manera de resolver el problema, sin utilizar la recursividad, se basa en el hecho de que para obtener la solución más corta, es necesario mover el disco más pequeño en todos los pasos impares, mientras que en los pasos pares solo existe un movimiento posible que no lo incluye. El problema se reduce a decidir en cada paso impar a cuál de las dos pilas posibles se desplazará el disco pequeño. El algoritmo en cuestión depende del número de discos del problema:

Si inicialmente se tiene un número impar de discos, el primer movimiento debe ser colocar el disco más pequeño en la pila destino, y en cada paso impar se le mueve a la siguiente pila a su izquierda (o a la pila destino si está en la pila origen). La secuencia será: destino, auxiliar, origen, destino, auxiliar, origen, etc.
Si se tiene inicialmente un número par de discos, el primer movimiento debe ser colocar el disco más pequeño en la pila auxiliar, y en cada paso impar se le mueve a la siguiente pila a su derecha (o a la pila origen si está en la pila destino). La secuencia será: auxiliar, destino, origen, auxiliar, destino, origen, etc.

Una forma equivalente de resolverlo es la siguiente: coloreando los discos pares de un color y los impares de otro, y se resuelve el problema añadiendo la siguiente regla: no colocar juntos dos discos de un mismo color. De esta manera, solo queda un movimiento posible (además del de volver hacia atrás).